【 難易度:★★★★☆ 】
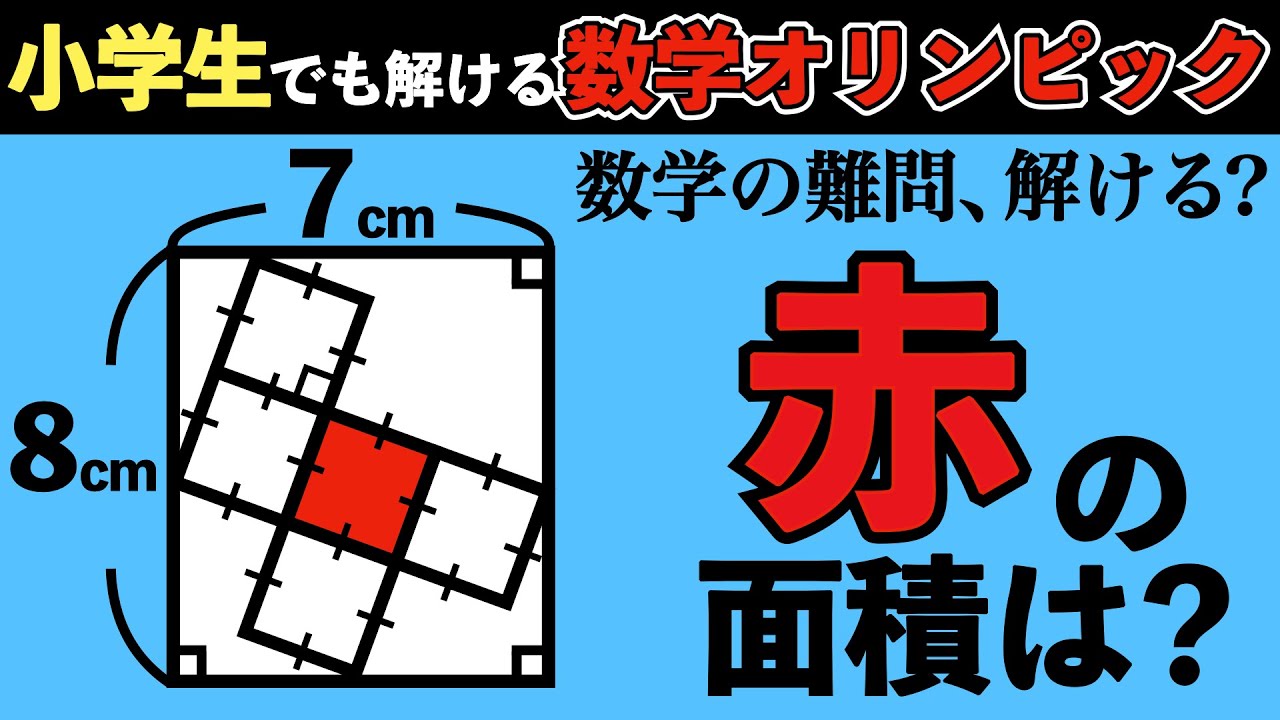
2001年の日本数学オリンピックの予選問題です。
▼重要な解法ポイント
①まずは正方形で足りなさそうなものを付け足していきましょう。ぱっと見で正方形が9つ見えたらなかなか補助線を引くセンスがあるかもしれません。
②正方形が9つになると、問題の7×8の長方形を拡張して9つの正方形に接するような四角形を作ることができると思います。拡張した四角形を⚪︎+×=90°の関係性で紐解いていくと、拡張してできて四角形が正方形であることが分かるはずです。
③拡張してできた正方形(大正方形)の上の辺と小さい正方形が接している点をA、大正方形の下の辺と小さい正方形が接している点をBとします。ABと同じ線分を大正方形の左右の辺でも同じように作ることができると思います。このことから大正方形の1辺の長さが9cmであることがわかるはずです。
④大正方形のうち、9つの正方形以外の部分が同じ直角三角形4つでできていることに着目して、そのうちの一つの直角三角形と同じ形の図形が直角三角形の中にあることがわかります。どのような長さの比になっているのかを知ることによって、直角三角形の一つの面積を算出することができます。
⑤大正方形の面積は③でわかり、直角三角形1つの面積が④で分かったので、求める部分の面積を算出することができます。
小学生が解くにはかなりタフな問題だったと思いますが、これまでのまなびスクエアでの要素をどんどん使っていくことで解くことができる問題となっていました。
数学オリンピックの問題であるにも関わらず、小学生でも解けるというのはなかなか面白い問題でしたね。
改めて算数が面白いと感じる瞬間でした。
▼manavisquare(まなびスクエア)に関する各ページはこちら
・HP
https://manavigate.co.jp/
・manavisquare(オンライン家庭教師プラットフォーム)
https://mnsq.jp/
・twitter
Tweets by manavisquare
・菅藤 佑太のtwitter
Tweets by mrkeiosfc16no1
▼お気軽にお問合せください!
kikaku@mnsq.jp
#中学受験 #算数 #図形