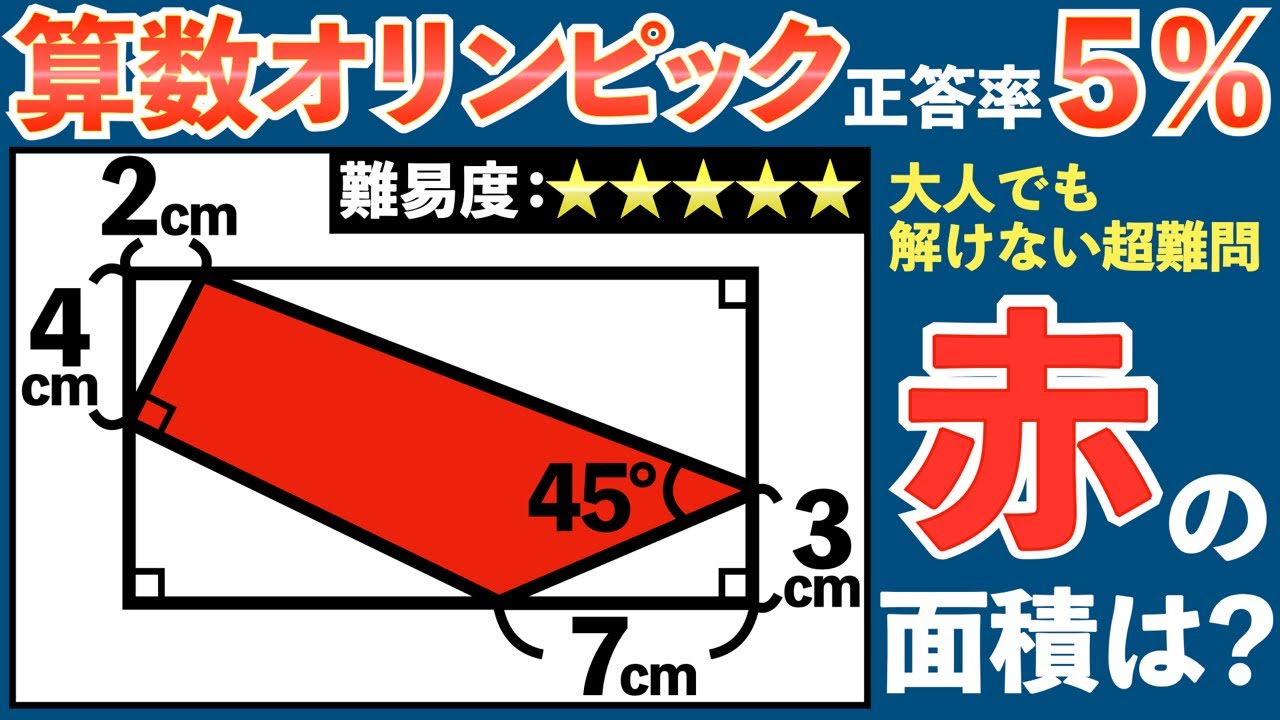
【 難易度:★★★★★ 】
2006年の算数オリンピックの問題です。
▼重要な解法ポイント
①まずは前提条件といきたいところですが、何もすることがありませんね。困りました。こういう時に活躍するのは角度に名前をつけていくことです。分からない角度を「⚪︎」「×」と置いたりしてみましょう。直角三角形が見えるので、三角形の内角の和が180°であることから「⚪︎+×+90°=180°」となることを押さえておくことがポイントです。他の直角三角形にもどんどん記号を書いていきましょう。左上の直角三角形が左下の直角三角形と同じ形の直角三角形と同じ形になることがわかれば上出来です。
②右下の直角三角形に注目しましょう。図形全体の長方形の中にできた四角形の内角の中で45°が見えて、これを活用してみようと考えたあなた、間違い無く天才です。この45°を使って、「⚪︎+×+90°=180°」の法則を活用していきましょう。そうすると補助線が見えてくるはずです。長方形の中に長方形(はたまた正方形)が見えたらかなり筋が良いと思います。
③ここからは同じ形の図形のオンパレードです。同じ形の図形のポイントとしては、対応する辺の長さでしたね。同じ形の図形の辺の長さの比をここで詳らかにしていきましょう。そうすると図形全体の長方形の縦と横の長さの関係を導くことができるはずです。あとはパズル的に長方形の縦と横の長さを算出しましょう。
④長方形全体の面積、求める部分以外の直角三角形の面積を全て求めることができるので、「(求める部分の面積)=(全体)ー(求める面積部分以外の面積)」という面積の考え方から、求める部分の面積を算出することができます。
「⚪︎+×+90°=180°」、「同じ形の図形」、「(求める部分の面積)=(全体)ー(求める面積部分以外の面積)」、「比(単位)を揃える」が出現する、まさに図形問題の要素をギチギチに詰めたような問題でしたね。
知識があるだけでは解けず、要素を知っているからこそ引ける補助線があるので、試行錯誤しながら補助線を引く難しさもありました。
文句なしの超難問でしたね。かといってとんでもなく難しい要素だけが散りばめられているわけではないので、ギリギリ小学生が解ける範囲のとんでもなく良い問題だったと思います。
▼manavisquare(まなびスクエア)に関する各ページはこちら
・HP
https://manavigate.co.jp/
・manavisquare(オンライン家庭教師プラットフォーム)
https://mnsq.jp/
・twitter
Tweets by manavisquare
・菅藤 佑太のtwitter
Tweets by mrkeiosfc16no1
▼お気軽にお問合せください!
kikaku@mnsq.jp
#中学受験 #算数 #図形