【 難易度:★★★☆☆ 】
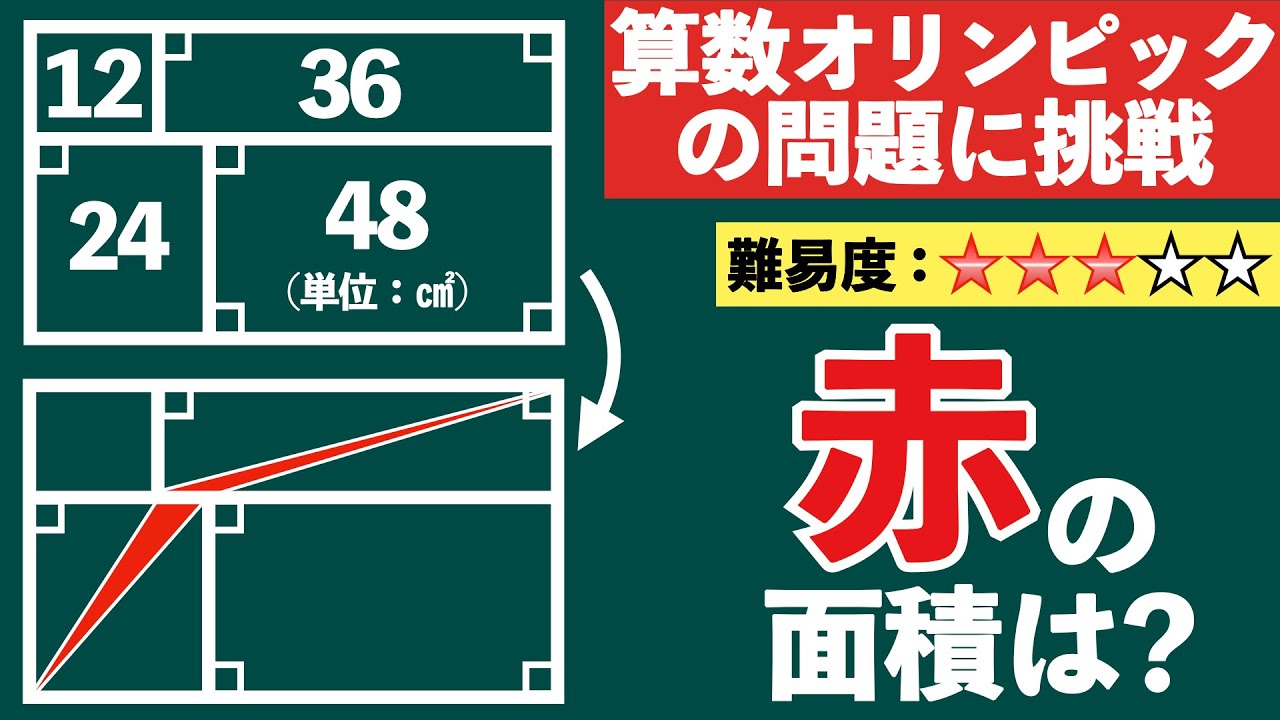
1999年の算数オリンピックの問題です。
▼重要な解法ポイント
①まずは面積の情報から長さの情報に変換していきましょう。ポイントは2つの長方形において縦の長さが同じ場合、横の長さの比が面積の比になるというところです。
②上の部分の長方形と下の部分の長方形の長さの情報が分かったら、それぞれの長さの指標を合わせる作業をしていきましょう。コツは最小公倍数です。単位合わせを意識しましょう。
③ここまできたらあとは三角形の面積を求めていきます。今回必要になるのは等積変形です。等積変形のコツは底辺の長さと高さに着目することです。底辺も高さもどちらも同じ長さであれば面積が同じになるのは当たり前のことですよね。この特性を活用して図形を変形していきます。あとは求める部分の面積の算出は難しくないですよね。
面積の情報のみから長さの比の情報に次々と変換していくパズル的な問題でした。
最後は等積変形などを使いながら上手く面積を算出していくので、かなり基礎的な要素が盛りだくさんの問題でしたね。
長方形な三角形の面積の求め方がきちんと理解できていないと、なかなかとっかかりにくかったのではないでしょうか。
▼manavisquare(まなびスクエア)に関する各ページはこちら
・HP
https://manavigate.co.jp/
・メンバーシップ
https://www.youtube.com/channel/UCWj73Vd9tI7mKmnTjdZeDJQ/join
・manavisquare(オンライン家庭教師プラットフォーム)
https://mnsq.jp/
・twitter
Tweets by manavisquare
・菅藤 佑太のtwitter
Tweets by mrkeiosfc16no1
▼お気軽にお問合せください!
kikaku@mnsq.jp
#中学受験 #算数 #図形